Cílem této práce je prozkoumat potenciál metod založených na rezoluci pro uvažování s lineárním časem. To na abstraktní rovině znamená navrhnout nové algoritmy pro automatické uvažování o vlastnostech systému, které se vyvíjí v čase. Konkrétně v této práci ukážeme,
Navržené myšlenky byly implementovány a práce obsahuje výsledky experimentů, které na reprezentativních množinách benchmarků prokazují jejich praktický potenciál. Náš systém LS4 se ukázal býti jedním z nejsilnejších veřejně dostupných LTL dokazovačů. Zmíněné vylepšení algoritmu PDR podstatně zvyšuje výkon naší implementace pri verifikaci hardware v multi-property módu. Dá se předpokládat, že ostatní implementace mohou z nové techniky benefitovat podobným zpusobem. V neposlední řadě náš plánovač PDRplan obstál při porovnání s nejmodernejšími plánovači na benchmarcích z mezinárodní plánovací souteže IPC s velmi slibným výsledkem.
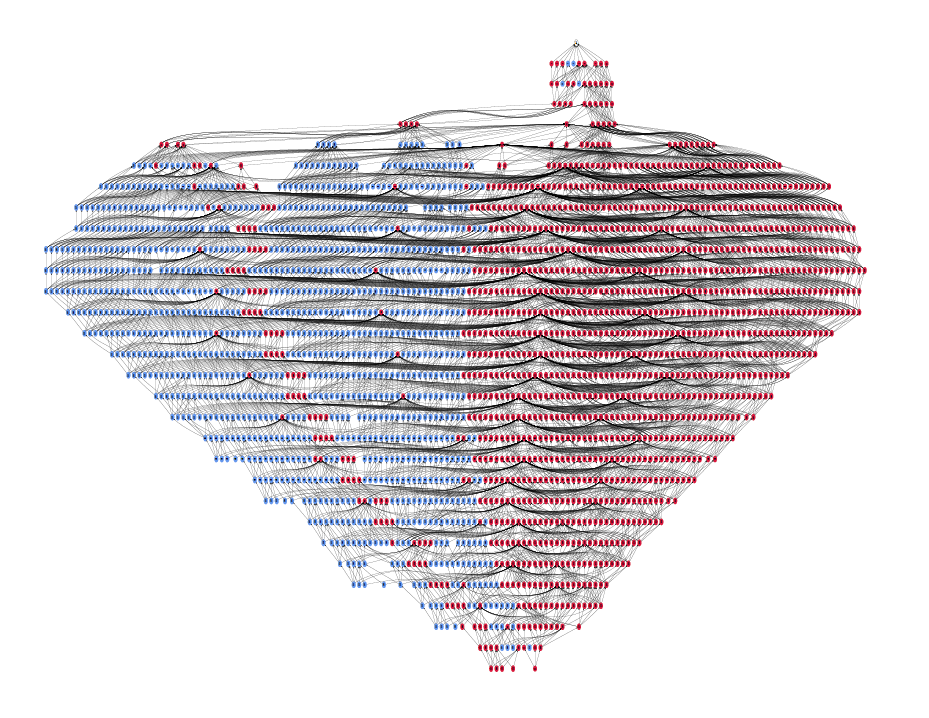
Vrstvy klauzulí vygenerovaných algoritmem Reach (popsaným v páte kapitole disertace) na problému bobsmminiuart z kolekce soutěže Hardware Model Checking Competition.
Ilustrace zachycuje situaci na konci 30. iterace běhu algoritmu. V tomto okamžiku algoritmus ukázal, že v problému neexistuje chybový běh do délky 30 kroků. Červeně jsou zvýrazněné ty klauzule, které byly použity v posledním (částečném) důkazu (pro délku běhu 30). Ostatní klauzule byly vygenerovány během předchozích iterací.
Spojení mezi klauzulemi vyznačují logickou závislost.
Čísla klauzulí byla jednoznačně přiřazena. Klauzule s určítým číslem se může objevit ve více vrstvách. Objevení dvou identických vrstev by znamenalo, že neexistuje chybový běh žádné (konečné) délky a zadaný problém je tedy nesplnitelný.
[Pro zvětšní klikněte na ilustraci.]