The aim of this thesis is to explore the potential of resolution-based methods for linear
temporal reasoning. On the abstract level, this means to develop new algorithms for automated
reasoning about properties of systems which evolve in time. More concretely, we
will:
- show how to adapt the superposition framework to proving theorems in propositional
Linear Temporal Logic (LTL),
- use a connection between superposition and
the CDCL calculus of modern SAT solvers to come up with an efficient LTL prover,
- specialize the previous to reachability properties and discover a close connection to Property
Directed Reachability (PDR), an algorithm recently developed for model checking of
hardware circuits,
- further improve PDR by providing a new technique for enhancing
clause propagation phase of the algorithm, and
- adapt PDR to automated planning
by replacing the SAT solver inside with a planning-specific procedure.
We implemented the proposed ideas and provide experimental results which demonstrate
their practical potential on representative benchmark sets. Our system LS4 is
shown to be the strongest LTL prover currently publicly available. The mentioned enhancement
of PDR substantially improves the performance of our implementation of the
algorithm for hardware model checking in the multi-property setting. It is expected that
other implementations would benefit from it in an analogous way. Finally, our planner
PDRplan has been compared with the state-of-the-art planners on the benchmarks from
the International Planning Competition with very promising results.
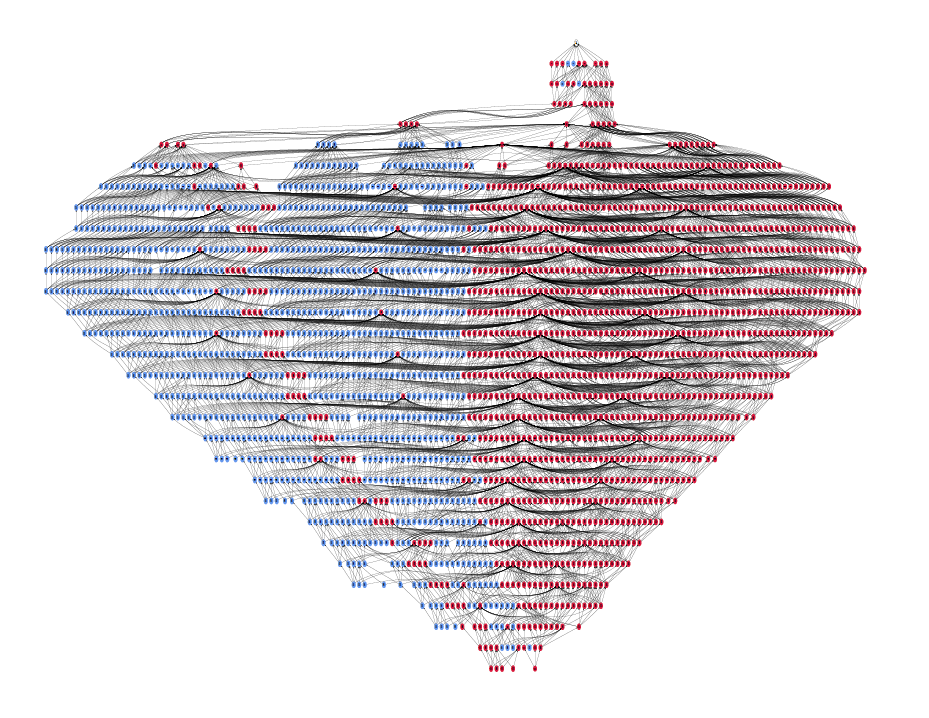
Layers of clauses generetad by the Reach algorithm (described in Chapter 5 of the thesis) on problem bobsmminiuart from the Hardware Model Checking Competition repository.
The figure captures situation at the end of iteration 30 of the run of the algorithm. At that point the algorithm has shown that there is not bug-trace of length 30 steps or less.
Clauses highlighted in red are those used in the last (partial) proof (for the lenght 30). The remaining ones were generated during previous iterations.
Links between clauses signify logical dependencies.
Numbers are uniquely assigned to clauses. A clause may occur in several layers.
Discovering two idential layers would mean that there is no bug-trace of any length and the problem is unsatisfiable.
[Click on the figure to enlarge.]



